22. 更多数学知识
这部分是额外赠送的选修材料,而不是必修课。如果你想知道我们如何推导出基于时间的反向传播算法最终累加方程,这部分将为你答疑解惑。
在之前的视频中,我们讨论了基于时间的反向传播算法。我们使用了很多偏导数,每个状态累加了误差变化的贡献。还记得吗?
我们需要一个基于时间的反向传播算法的总体方案时,我只是简单展示了这个方程,没有给出进一步的解释。
提醒一下,调整矩阵的权重时,推导以下两个方程式:W_s和矩阵W_x:
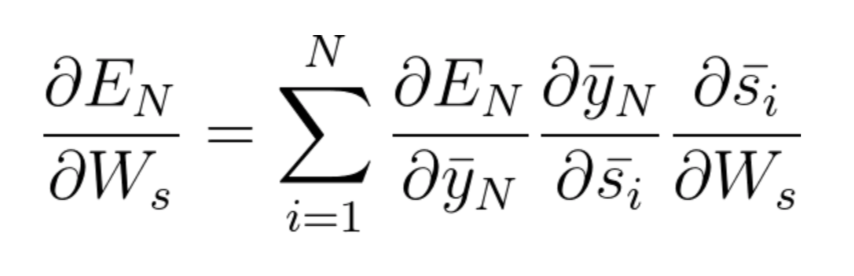
方程式48:调整Ws时基于时间的反向传播算法计算
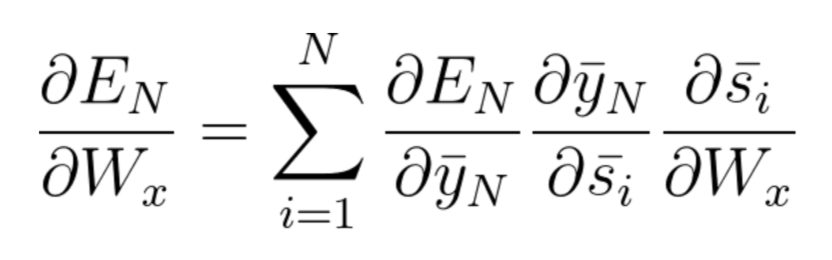
方程式49:调整Wx时基于时间的反向传播算法计算
为了总结这个例子,我们要避免证明方程式48和方程式49,而是侧重于整体框架。
观察下列概略图,该图展示了网络的一部分:
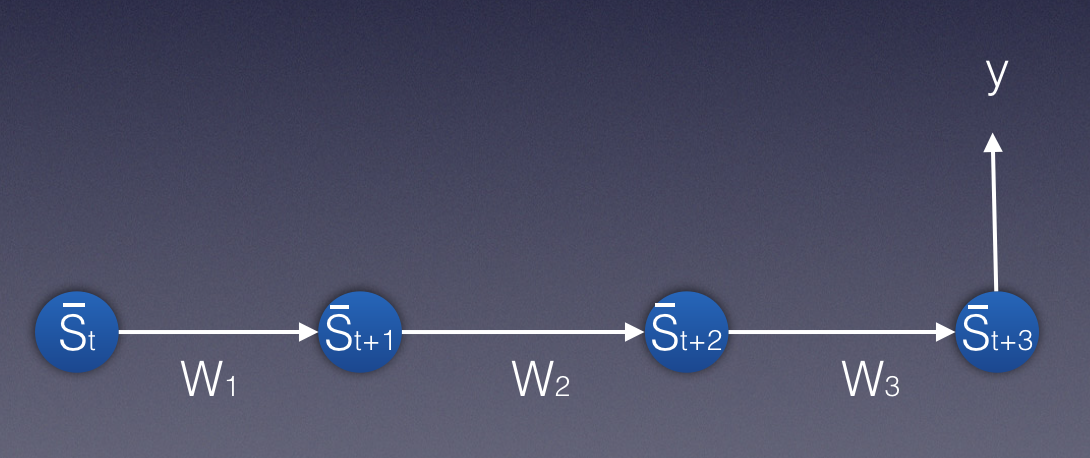
上图中,我们有四个状态,从s_t开始。
我们首先考虑三个权重矩阵:W_1、W_2和W_3作为三个不同的矩阵。
使用链式法则,我们可以推导出以下三个方程式:
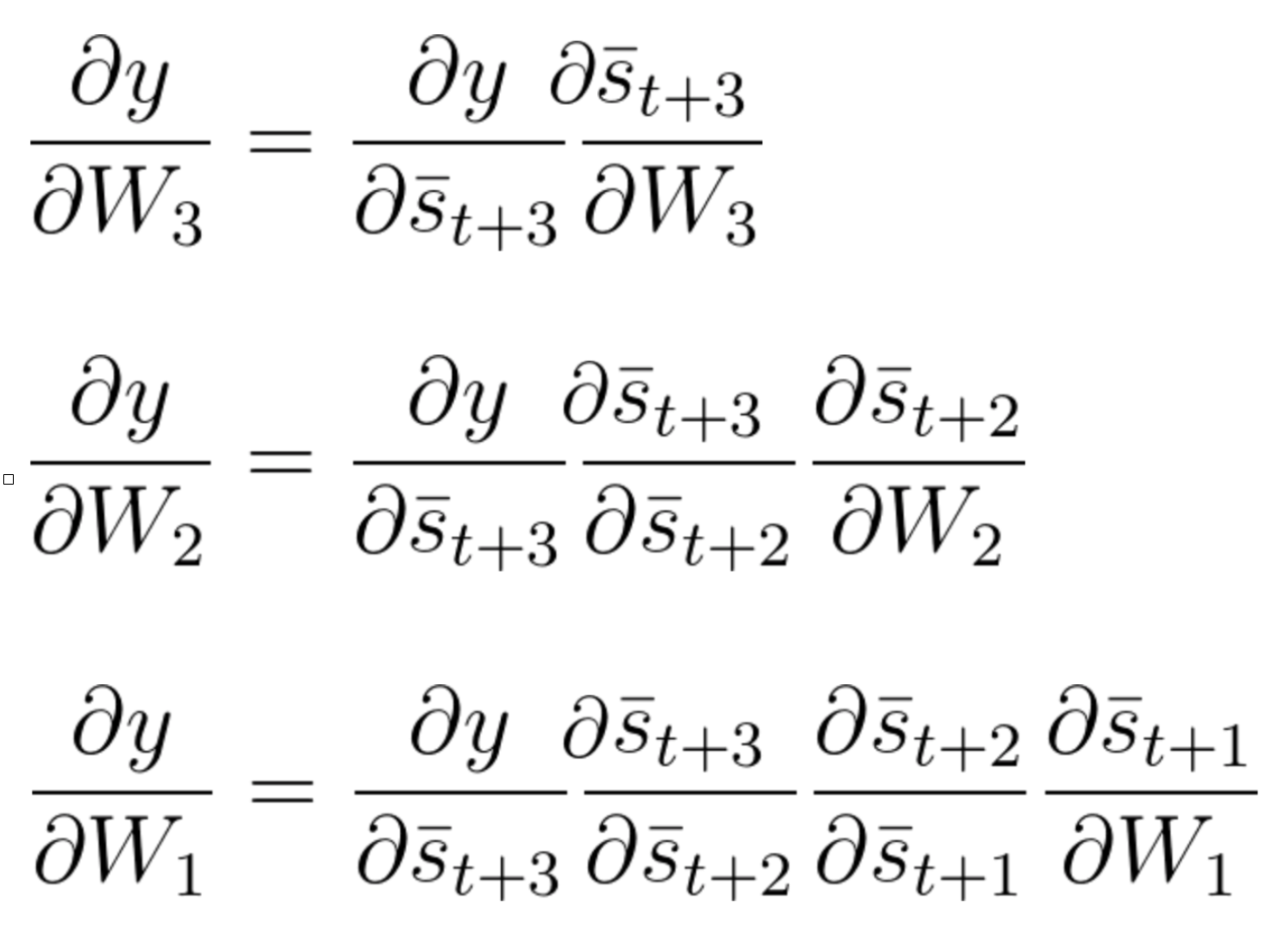
方程式 50 (方程组)
在基于时间的反向传播算法中我们累加贡献,因此:
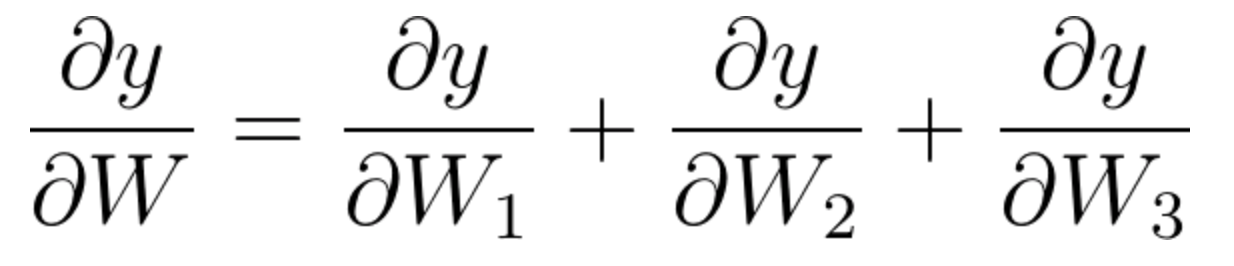
方程式 51
因为这个网络表现为基于时间的展开,所以我们明白连接每个状态的权重矩阵是相同的。因此:
方程式 52
通过方程式 52、方程式 51和我们推导出的方程组 50:
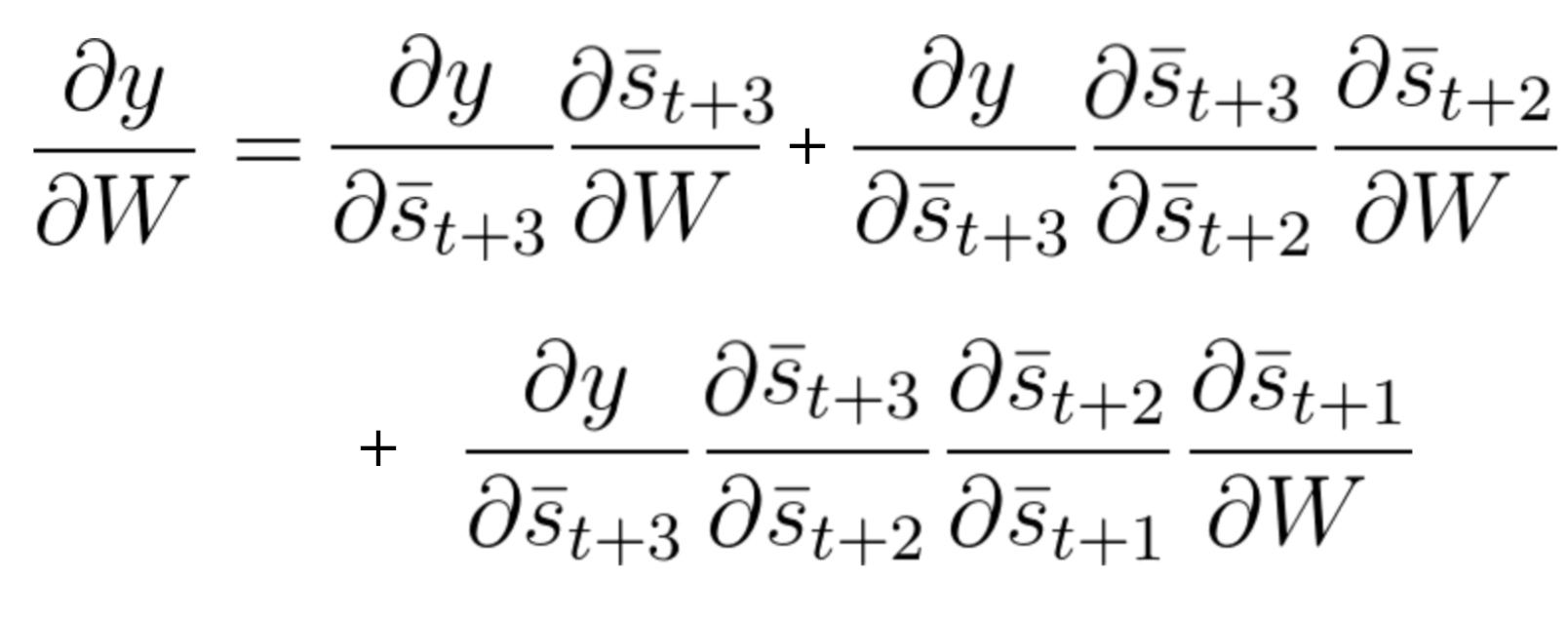
方程式 53
方程式 53总结了基于时间的反向传播算法(BPTT)的数学过程,可以简写为:
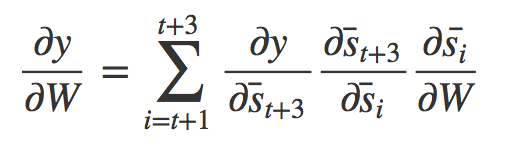
方程式 54
请注意,对于i=t+1,我们推导如下:
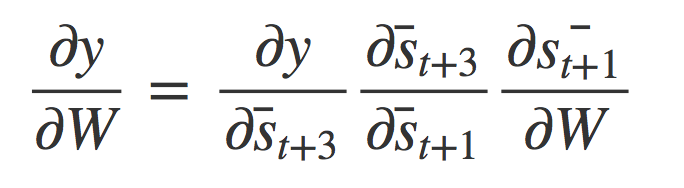
方程式 55
使用链式法则,我们可以推导出以下方程式(如方程组 50所示)。
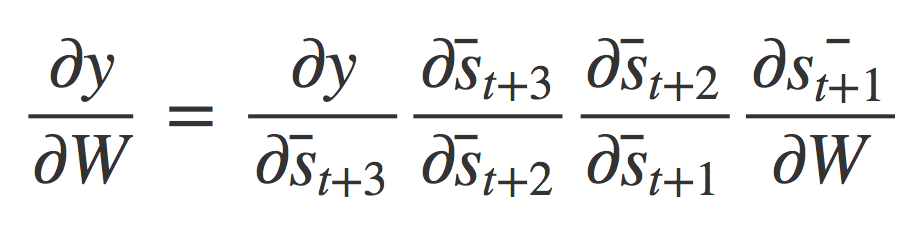
方程式 56
基于时间的反向传播算法计算的一般推导可以通过以下方式表示:
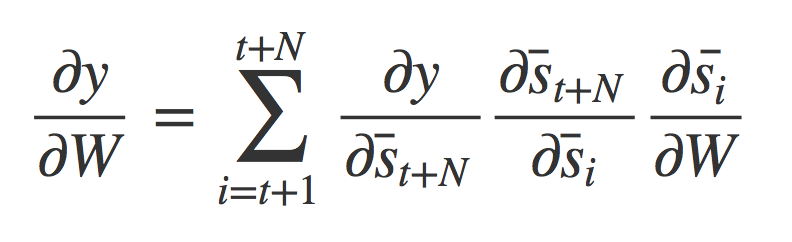
方程式 57